函 数
函数的定义
如果当变量x在其变化范围内任意取定一个数值时，量y按照一定的法则总有确定的数值与它对应，则称y是x的函数。变量x的变化范围叫做这个函数的定义域。通常x叫做自变量，y叫做因变量。
注：为了表明y是x的函数，我们用记号y=f(x)、y=F(x)等等来表示。这里的字母f、F表示y与x之间的对应法则即函数关系,它们是可以任意采用不同的字母来表示的。
注：如果自变量在定义域内任取一个确定的值时，函数只有一个确定的值和它对应，这种函数叫做单值函数，否则叫做多值函数。这里我们只讨论单值函数。
函数的表示
a)：解析法：用数学式子表示自变量和因变量之间的对应关系的方法即是解析法。
例：直角坐标系中，半径为r、圆心在原点的圆的方程是：x2+y2=r2
b)：表格法：将一系列的自变量值与对应的函数值列成表来表示函数关系的方法即是表格法。
例：在实际应用中，我们经常会用到的平方表，三角函数表等都是用表格法表示的函数。
c)：图示法：用坐标平面上曲线来表示函数的方法即是图示法。一般用横坐标表示自变量，纵坐标表示因变量。
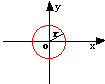
例：直角坐标系中，半径为r、圆心在原点的圆用图示法表示为：
函数的简单性态
函数的有界性
如果对属于某一区间I的所有x值总有│f(x)│≤M成立，其中M是一个与x无关的常数，那么我们就称f(x)在区间I有界，否则便称无界。
注意：一个函数，如果在其整个定义域内有界，则称为有界函数。
例如：函数cosx在(-∞,+∞)内是有界的.
函数的单调性
如果函数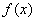
在区间(a,b)内随着x增大而增大，即：对于(a,b)内任意两点x1及x2，当x1＜x2时，有
，
则称函数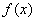在区间(a,b)内是单调增加的。
如果函数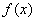在区间(a,b)内随着x增大而减小，即：对于(a,b)内任意两点x1及x2，当x1＜x2时，有
，
则称函数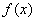在区间(a,b)内是单调减小的。
例如，函数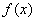=x2在区间(-∞,0)上是单调减小的，在区间(0,+∞)上是单调增加的。
函数的奇偶性
如果函数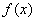对于定义域内的任意x都满足
＝，
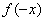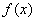则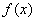叫做偶函数；
如果函数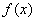对于定义域内的任意x都满足
＝-，
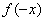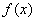则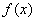叫做奇函数。
注意：偶函数的图形关于y轴对称，奇函数的图形关于原点对称。
函数的周期性
对于函数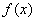，若存在一个不为零的数l，使得关系式
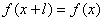
对于定义域内任何x值都成立，则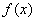叫做周期函数，l是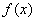的周期。
注：我们说的周期函数的周期是指最小正周期。
例如：函数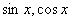
是以2π为周期的周期函数；函数tgx是以π为周期的周期函数。
反函数
反函数的定义
设有函数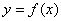
，若变量y在函数的值域内任取一值y0时，变量x在函数的定义域内必有一值x0与之对应，即
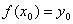，那末变量x是变量y的函数.
这个函数用来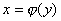
表示，称为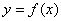函数的反函数.
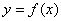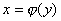注：由此定义可知，函数也是函数的反函数。
反函数的性质
在同一坐标平面内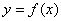，与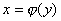的图形是关于直线y=x对称的。
例题：
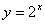函数
与函数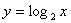
互为反函数，则它们的图形在同一直角坐标系中是关于直线y=x对称的。如下图所示：
