函数的微分
学习函数的微分之前，我们先来分析一个具体问题：
一块正方形金属薄片受温度变化的影响时，其边长由x0变到了x0+△x，则此薄片的面积改变了多少？
解答：设此薄片的边长为x，面积为A，则A是x的函数：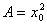
薄片受温度变化的影响面积的改变量，可以看成是当自变量x从x0取的增量△x时，函数A相应的增量△A，
即：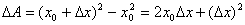
从上式我们可以看出，△A分成两部分，第一部分是△x的线性函数，即下图中红色部分；
第二部分即图中的黑色部分，
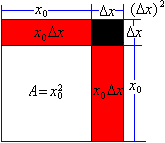
当△x→0时，它是△x的高阶无穷小，表示为：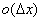 
由此我们可以发现，如果边长变化的很小时，面积的改变量可以近似的用地一部分来代替。
下面我们给出微分的数学定义：
函数微分的定义
设函数在某区间内有定义，x0及x0+△x在这区间内，若函数的增量可表示为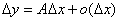
，其中A是不依赖于△x的常数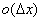，是△x的高阶无穷小，则称函数在点x0可微的。
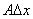叫做函数
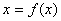在点x0相应于自变量增量△x的微分，记作dy，
即：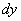
=
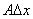
通过上面的学习我们知道：微分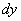是自变量改变量△x的线性函数，dy与△y的差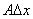是关于△x的高阶无穷小量，我们把dy称作△y的线性主部。
于是我们又得出：
当△x→0时，△y≈dy.
导数的记号为：
，
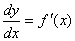现在我们可以发现，它不仅表示导数的记号，而且还可以表示两个微分的比值(把△x看成dx,即：定义自变量的增量等于自变量的微分)，还可表示为：
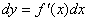
由此我们得出：若函数在某区间上可导，则它在此区间上一定可微，反之亦成立。
微分形式不变性
什么是微分形式不变性呢？
设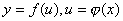
，则复合函数
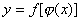的微分为：
，
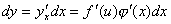由于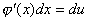
，故我们可以把复合函数的微分写成
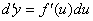
由此可见，不论u是自变量还是中间变量，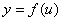
的微分dy总可以用
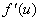与du的乘积来表示，
我们把这一性质称为微分形式不变性。
例题：已知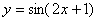
，求dy
解答：把2x+1看成中间变量u，根据微分形式不变性，则
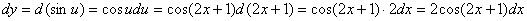
通过上面的学习，我们知道微分与导数有着不可分割的联系，前面我们知道基本初等函数的导数公式和导数的运算法则，那么基本初等函数的微分公式和微分运算法则是怎样的呢？
下面我们来学习——基本初等函数的微分公式与微分的运算法则
高等数学在线教程
同济大学高等数学精品课程
上海交大高等数学课程
高等数学复习教程
